Control Estadístico del Proceso - Gráficas de Control

Algunas personas se sorprenden al enterarse que dos partes aparentemente idénticas, hechas bajo condiciones cuidadosamente controladas, de la misma fuente de materia prima y fabricadas sólo con diferencia de segundos por la misma máquina y operador, puedan ser diferentes en muchos aspectos.

En realidad, cualquier proceso de fabricación, aún el más confiable, se caracteriza por cierto grado de variabilidad que es de naturaleza aleatoria y que no se puede eliminar completamente. En la prestación de servicios y en los procesos administrativos esta variabilidad también está presente.

Cuando la variabilidad presente en un proceso de realización de un producto o servicio está limitada a la variación natural y aleatoria, se dice que el proceso está Bajo Control Estadístico.

Esto se consigue buscando y eliminando todas las causas que originan variaciones de otra clase, como son las que se pueden deber a operadores poco entrenados, materias primas de baja calidad, ajustes indebidos de las máquinas, falta de control de las condiciones ambientales, partes desgastadas, deterioro en el herramental, instrucciones poco claras, etc.

Como los procesos de fabricación o de servicios raramente se encuentran libres de este tipo de factores, es importante el contar con algún método sistemático de detectar las desviaciones notables de un estado de control estadístico, cuando estas se presentan o si es posible antes. Es para este fin para el que se emplean principalmente las gráficas de control.

Una gráfica de control consiste en una línea central que corresponde al promedio en que se desarrolla el proceso y dos líneas correspondientes a los límites de control estadístico superior e inferior.

Estos límites se calculan a partir de un conjunto de datos representativos y funcionan de tal forma que los valores que caen fuera de ellos deben ser interpretados como indicaciones de una falla de control o lo que es lo mismo de variación excesiva o inestabilidad del proceso. No deben ser confundidos con los límites de especificación los cuales fueron escogidos por el cliente o la ingeniería para cumplir un objetivo arbitrario.

Marcando los resultados obtenidos de muestras tomadas periódicamente en intervalos frecuentes, es posible verificar, por medio de esta gráfica, si el proceso está bajo control o si en el proceso ha aparecido alguna falla que causa problemas como los indicados anteriormente. 

Cuando un punto obtenido cae fuera de los límites de control, se buscan fallas, pero si aún los puntos quedan dentro de los límites, la aparición de una tendencia o irregularidad sistemática puede servir como aviso de que se debe tomar alguna acción para evitar problemas más serios. 

La capacidad para “leer” o interpretar adecuadamente las gráficas de control y determinar justamente qué acción correctiva y preventiva debe tomarse, es cuestión de objetividad, experiencia y buen juicio por parte de los dueños de los procesos.

Hay varios tipos de gráficas de control que pueden construirse. Si se obtienen datos para una característica de calidad que puede medirse y expresarse en números, generalmente se utilizan gráficas de control por variables para mediciones de tendencia central y variabilidad, ya que la calidad de un producto o servicio, frecuentemente puede resumirse en términos de estas dos cantidades.

La secuencia de decisiones y actividades para implantar el uso y aprovechamiento de un gráfico de control de procesos incluirá comúnmente la mayoría de los siguientes puntos: 

1. Decisiones antes de preparar las gráficas de control.

• Objetivo de las gráficas. La finalidad es complementar y mejorar la capacidad de análisis del proceso de los operadores y supervisores con el objetivo de:
• • Establecer o cambiar las especificaciones o para determinar si un proceso puede o no cumplir con las mismas, establecer o cambiar procedimientos de producción eliminando causas especiales de variación y establecer o cambiar procedimientos de inspección y/o aceptación.
  • Servir como base para decidir si, durante el curso de la producción, se deben buscar las causas de la variación y corregirlas o se debe permitir que el proceso continúe como está.
  • Servir como base para decidir la aceptación o rechazo en línea de un producto en particular.
  • Hallar oportunidades de mejora continua o reducción de costos.

• Elección de la variable. El que una variable sea fácil de muestrear y medir no justifica por sí solo la elaboración de un gráfico de control. Sobre todo al principio es importante seleccionar variables que ofrezcan posibilidades para generar el tipo de ahorros que todos los supervisores y directores reconozcan con facilidad.

• Elección de la base de formación de subgrupos. La clave del funcionamiento del gráfico de control está en la formación racional de subgrupos de muestras. Esto requiere el uso del criterio adecuado al tipo de producción y a la finalidad buscada con el gráfico. Generalmente los subgrupos se deben seleccionar de tal modo que cada subgrupo sea lo más homogéneo posible y que ofrezca máxima oportunidad de variación entre subgrupos.

• Decisión del tamaño y frecuencia de los subgrupos. Debido a que se pretende que la variación dentro de cada subgrupo sea mínima es deseable que los subgrupos sean lo más pequeños que se pueda. Desde un punto de vista estadístico, un tamaño de subgrupo de cuatro es suficiente para que la distribución de las medias sea casi normal. A mayor tamaño de subgrupo mayor será la estrechez de los límites de control de la gráfica de medias. Con respecto a la frecuencia de los subgrupos no se establecen reglas, pero se recomienda una toma de muestras más frecuente durante las etapas iniciales la cual puede irse reduciendo conforme el proceso se va estabilizando. Si el costo del muestreo es relativamente alto, la frecuencia de muestreo, debe equilibrarse con los beneficios esperados.

• Método y formatos para registro de los datos. Para efectos de aprendizaje y sensibilización de los operadores podría resultar interesante trabajar los primeros gráficos con papel y lápiz, sin embargo, es más eficiente la utilización rutinaria de computadoras ya que se reducen los errores y se dispone de más tiempo para el análisis. Cualquier formato que se utilice debe contar con espacio para anotar observaciones y comentarios que redondeen el contexto de los datos.

• Determinación del método de medición. Debe asegurarse formalmente la calidad de los datos obtenidos del sistema de medición (instrumentos y equipo, operadores y métodos) antes de intentar extraer conclusiones válidas de los gráficos de control elaborados con esos datos.

2. Iniciación de las gráficas de control.

• Efectuar y registrar las mediciones. No debe olvidarse que el gráfico de control mostrará no solo la variabilidad de la característica de calidad que se mide sino también la variabilidad del proceso de medición mismo. Debe evitarse al máximo la introducción de errores de medición o de registro. Siempre debe conservarse el orden temporal de las mediciones. Junto a los datos debe anotarse cualquier ocurrencia que pueda ayudar a encontrar causas especiales en caso de ser necesario.

• Calcular las estadísticas del subgrupo. Dependiendo del tipo de gráfica será necesario calcular la media, el rango, la desviación estándar o algún otro estadístico para cada subgrupo. Las fórmulas necesarias se presentan más adelante.

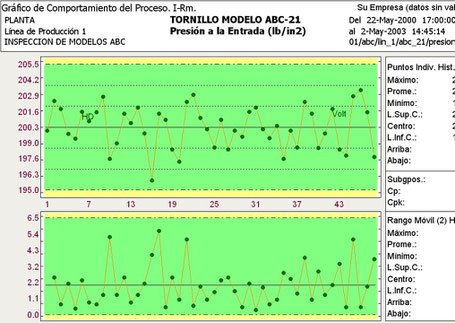
• Trazo de las gráficas. Aunque no es obligatoria, existe la práctica generalizada de presentar primero la gráfica de medias X y debajo de ella la gráfica de variabilidad ya sean rangos o desviaciones. Las escalas verticales se emplean para las medidas estadísticas y la escala horizontal es para los números de los subgrupos aunque pueden usarse fechas o números de lote. Cada punto en la gráfica representa el estadístico de un subgrupo. Los puntos pueden conectarse mediante líneas rectas pero algunos autores recomiendan no hacerlo para evitar que el gráfico asemeje demasiado a un gráfico de tendencias. El trazo de los puntos debe hacerse de inmediato a la toma de las mediciones de preferencia por los mismos operadores de los procesos ya que de la agilidad en la toma de decisiones pueden depender los beneficios que se obtengan del uso de la gráfica.

3. Determinación de los límites de control iniciales.

• Decisión del número de subgrupos requerido para calcular los límites de control. Estadísticamente es deseable contar con al menos 25 subgrupos para efectuar el cálculo de límites de control. En los procesos en los que la recolección de los datos no pueda hacerse rápidamente pueden calcularse límites preliminares a partir de 10 subgrupos para irlos refinando conforme se cuente con mayor información. Debe entenderse que estos límites preliminares no serán del todo confiables.

• Cálculo de los límites de control iniciales. En todos los casos los límites de control abarcan un espacio de probabilidad de 3 desviaciones estándar a cada lado de los valores promedio de los estadísticos de centramiento y variabilidad. Este espacio representa un buen equilibrio práctico y económico entre los dos tipos de errores que pueden cometerse al usar las gráficas para determinar la estabilidad de un proceso: el error de buscar un problema cuando no lo hay y el error de dejar correr el proceso cuando el problema existe realmente. Más adelante se enumeran los métodos que proporciona la teoría estadística para calcular o estimar la desviación estándar en cada tipo de gráfica.

• Trazo de las líneas centrales y los límites en las gráficas. Convencionalmente se acostumbra trazar las líneas centrales correspondientes al promedio de medias, rangos o desviaciones mediante una línea horizontal continua. A ambos lados de esta línea se trazan los límites de control con líneas horizontales discontinuas. En las gráficas de rangos o desviaciones los límites inferiores de control no se dibujan si son negativos. Para realizar análisis más detallados es de utilidad dividir con líneas más suaves el espacio entre la línea central y cada límite en tres secciones iguales que corresponden a las zonas de 1, 2 y 3 desviaciones estándar.

4. Obtención de conclusiones preliminares con las gráficas.

• Indicación de control o de falta de control. La falta de control se indica por los puntos que caen fuera de los límites de control. El diseño del cálculo de los límites de control ofrece un gran margen de confianza de que un sistema de causas comunes muy rara vez ocasionará que haya puntos fuera de los límites de control. Por el contrario, el solo hecho de que todos los puntos caigan dentro de los límites no es suficiente para decir que el proceso se encuentra bajo control. Todavía es necesario buscar tendencias, corridas o patrones en los datos que puedan señalar causas asignables de variación. Para esta investigación adicional se puede utilizar un conjunto de reglas basadas en la cantidad de puntos que cabría esperar que cayesen en cada zona del gráfico si el proceso estuviera sometido exclusivamente a un sistema de causas comunes. Las siguientes situaciones justifican la búsqueda de causa especiales de variación:

• Interpretación de los procesos que están bajo control. Cuando la gráfica indique que un proceso está en control estadístico sabremos que este proceso ha alcanzado, bajo las actuales circunstancias, su máximo potencial de realización del producto o servicio y estaremos en condiciones de comparar este desempeño con las especificaciones del cliente. Si las especificaciones son cumplidas entonces bastará con mantener el proceso como está para asegurar la calidad del producto o servicio. Si las especificaciones no son cumplidas entonces será necesario modificar profundamente el proceso mismo para reducir la variabilidad común y/o mejorar el centramiento.

• Interpretación de los procesos que están fuera de control estadístico. Cuando la gráfica indica que el proceso está fuera de control, la medida que se debe tomar es buscar las causas asignables de la variación y tratar de corregirlas. Los valores de centramiento y dispersión obtenidos no pueden utilizarse para comparar con las especificaciones del cliente debido a que el proceso no es estable ni predecible. A pesar de lo anterior es posible recalcular los límites de control eliminando de la gráfica los puntos fuera de control y de esa manera llegar a los valores que se tendrían si las causas especiales no estuviesen presentes. De esta manera podría analizarse si de cualquier forma será necesaria una reingeniería del proceso para cumplir con el requisito del cliente.

5. Continuidad en el empleo de las gráficas.

• Revisión de la línea central y de los límites de control. Los límites de control iniciales sirvieron para determinar si las operaciones efectuadas con anterioridad estaban bajo control. La continuidad del empleo de las gráficas consiste en seguir comparando los subsecuentes datos con los límites y cada punto fuera de control utilizarlo como base para buscar una causa asignable de variación y actuar para eliminarla. Eventualmente, la acumulación de datos requerirá la revisión o enmienda de los límites ya sea para refinar los cálculos o simplemente porque se han efectuado cambios fundamentales en el proceso que han modificado el sistema de causas comunes que lo hacen variar.

• Actuación en el proceso mediante las gráficas de control. Si se continúa el empleo de las gráficas de control, puede haber tres clases diferentes de actuaciones en el proceso: 1) eliminación de las causas asignables de variación que están a la vista mediante puntos fuera de control, 2) establecimiento del promedio del proceso y 3) establecimiento de la dispersión del proceso. Una vez que un proceso ha quedado bajo control con promedio y dispersión satisfactorios la finalidad de la gráfica es ayudar a que continúe esta situación.

• Empleo de las gráficas para la aceptación del producto o servicio. A pesar de que existen numerosas técnicas para la aceptación o rechazo de un producto o servicio mediante la inspección de lotes aislados, actualmente se reconoce que es mucho mejor el ser capaces de decidir de una manera general si se puede confiar o no en que un proceso pueda producir el producto o servicio aceptable. Las gráficas de control pueden comprobar si lo que se está haciendo se está haciendo bien a la primera.

• Empleo de las gráficas para actuar sobre las especificaciones. La base de todos los límites de especificación debería ser el posible uso del producto para el cual se especifican los límites. Idealmente todos los límites de especificación deben ser absolutamente correctos desde el punto de vista de lo que realmente se necesita. Muchas veces los límites de especificación se hacen más estrechos de lo necesario porque no se ha dedicado el tiempo y el esfuerzo suficiente para averiguar lo que es necesario. Aquí intervienen consideraciones de optimización de costos que difícilmente pueden hacerse sin la información que proporciona el gráfico de control. Hay muchos casos en que la conclusión acertada derivada de la gráfica de control es cambiar las especificaciones.