SuperCEP ofrece las siguientes gráficas de Control por Variables:
- Gráfica X - R (de la media y el rango)
- Gráfica X - S (de la media y la desviación estándar)
- Gráfica Pi - Rm (de los puntos individuales y el rango móvil)
- Gráfica X – Rm – R (de la media, el rango móvil y el rango)
- Gráfica EWMA - R (De los promedios móviles exponenciales y el rango).

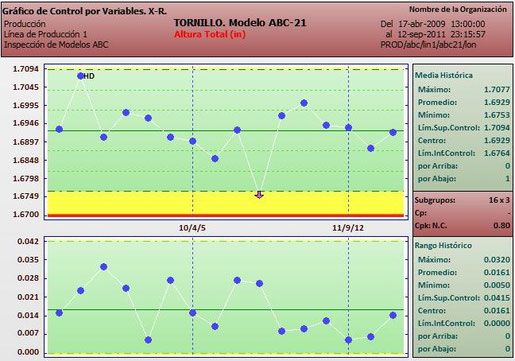
Gráfica de Medias y Rangos (X - R)
La gráfica X-R, que es la herramienta tradicional y fundamental del control estadístico de proceso, en realidad consiste de dos gráficas una para las Medias (X) que nos ayudará a controlar el centramiento del proceso y otra para los Rangos que nos ayudará a controlar su variabilidad. Estas medias y rangos son obtenidas de subgrupos de muestras de tamaño constante tomadas del proceso a intervalos regulares de tiempo o unidades de producción. Los tamaños de subgrupo más comunes son 4 ó 5. Cada punto de la gráfica de Medias es el promedio de las muestras de un subgrupo. Cada punto de la gráfica de Rangos es la diferencia entre el valor máximo y el mínimo de cada subgrupo. Los límites de control se calculan a partir del Rango promedio y delimitan una zona de 3 desviaciones estándar de cada lado de la media.
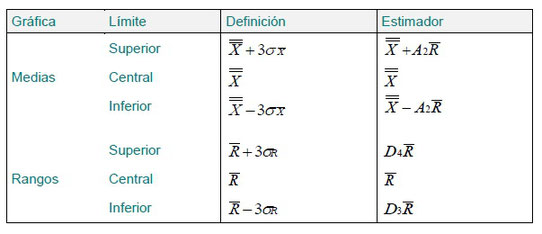
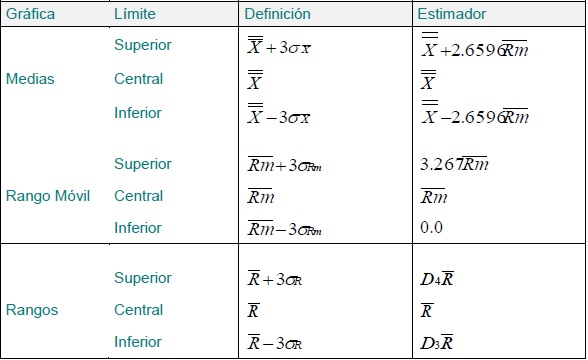
Las fórmulas necesarias para el cálculo de las líneas centrales y límites de control son:
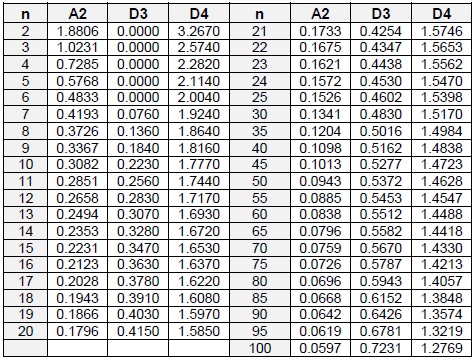
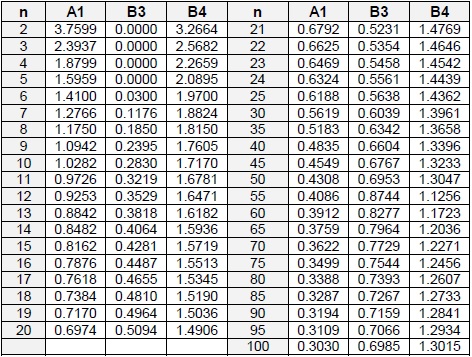
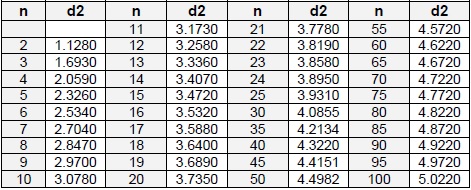
Los estimadores varían en función del tamaño del subgrupo n:
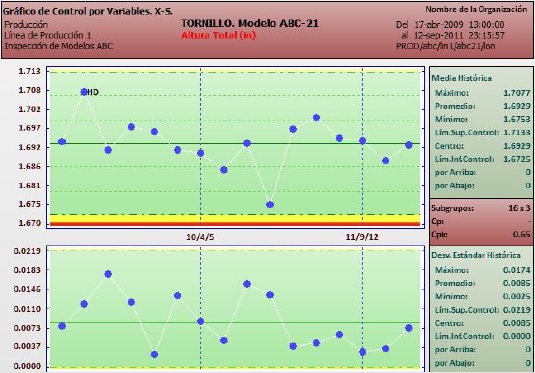
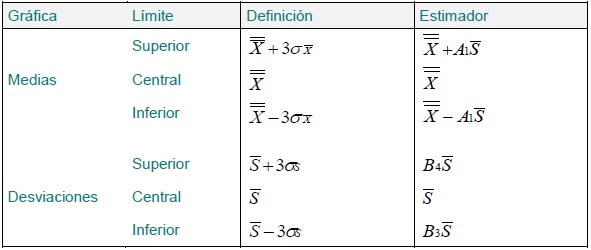
Gráfica de Medias y Desviaciones Estándar (X - S)
Cada punto de la gráfica de Medias es el promedio de las muestras de un subgrupo. Cada punto de la gráfica de Desviaciones es la desviación estándar interna de cada subgrupo. Los límites de control se calculan a partir de la Desviación estándar promedio y delimitan una zona de 3 desviaciones estándar de cada lado de la media.
Las fórmulas necesarias para el cálculo de las líneas centrales y límites de control son:
Los estimadores varían en función del tamaño del subgrupo n:
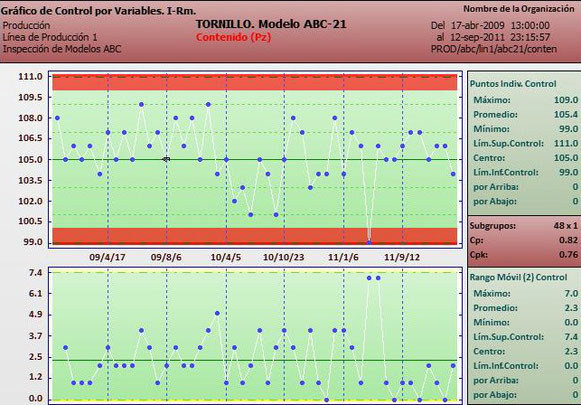
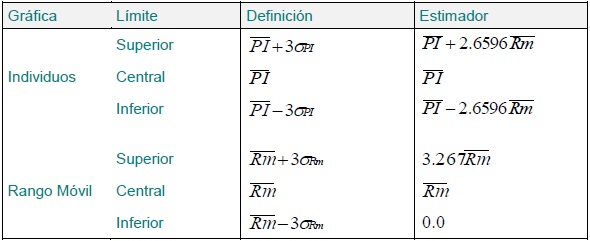
Gráfica de Individuos y Rangos Móviles (PI - Rm)
La gráfica de control de puntos individuales y rangos móviles puede utilizarse para características cuyas muestras individuales se distribuyan normalmente. En la gráfica PI cada punto representa un valor individual. En la gráfica Rm cada punto es la diferencia entre la muestra actual y la anterior.
Las fórmulas necesarias para el cálculo de las líneas centrales y límites de control son:
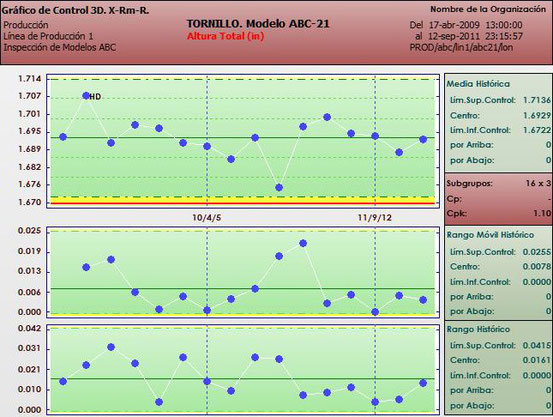
Gráfica de Medias, Rangos Móviles y Rangos (X-Rm-R ó 3D)
La independencia de las muestras que conforman cada subgrupo es uno de los requisitos más importantes para el correcto funcionamiento de los gráficos de control, pero también uno de los que con mayor frecuencia no se respeta. En ocasiones se hacen varias mediciones de la misma característica en la misma muestra y estas repeticiones se integran como subgrupos graficando su valor promedio y su rango. La no independencia de las repeticiones provoca que muchas veces el gráfico resultante no muestre control estadístico. La gráfica 3D pretende ayudar a solucionar este problema. Consiste en presentar las mismas gráficas de medias, rangos móviles y rangos que ya conocemos con una diferencia: los promedios de los subgrupos se toman como datos individuales para el gráfico de rango móvil y para el cálculo de límites en el gráfico de medias. Esta adaptación permite el cálculo de límites naturales más realistas.
Las fórmulas necesarias para el cálculo de las líneas centrales y límites de control son:
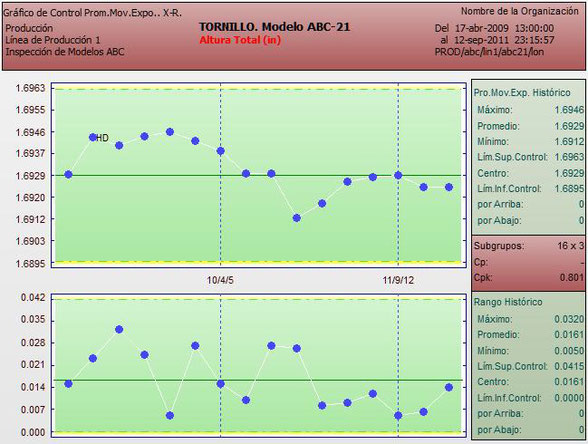
Gráfica de Promedios móviles exponenciales y Rangos (EWMA–R ó Rm)
La gráfica de Promedios Móviles Exponenciales es una alternativa a la gráfica de medias o a la de puntos individuales que puede utilizarse en procesos donde se desean investigar causas que provocan desplazamientos pequeños y constantes del centramiento del orden de 0.5 a 2.0 sigma. Cada punto de la gráfica es un valor ponderado geométricamente con todos los anteriores de forma que se representen mejor las tendencias a costa de la sensibilidad para cambios grandes o bruscos. Debe seleccionarse un factor de ponderación (lambda) entre 0.05 y 1.0 en función inversa del grado de suavizado que se quiere obtener. Los valores comunes están entre 0.2 y 0.4. Puede elaborarse con datos individuales o agrupados. La gráfica de rangos no sufre cambios.
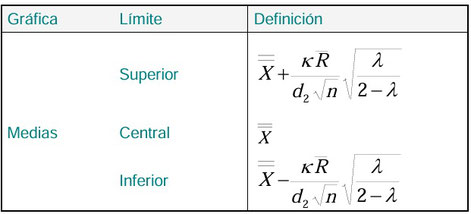
Las fórmulas necesarias para el cálculo de las líneas centrales y límites de control son:
El valor de d2 varía en función del tamaño del subgrupo n:
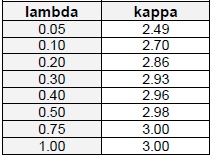
El valor de kappa varía en función de lambda:





Escribir comentario